Mission overview

The Gravity field and steady-state Ocean Circulation Explorer (GOCE) is the first Earth Explorer core mission of the European Space Agency (ESA). It was launched on 17 March 2009 from Plesetsk, Russia. The mission was dedicated to high-resolution gravity field determination and carried, as primary instrument, a three-axis gradiometer for determining the gravity field with a state-of-the-art accuracy of 1 mGal and the geoid with an accuracy of 1 cm, both at a spatial resolution of 100 km. In addition, the mission was equipped with two 12-channel dual-frequency LAGRANGE GPS/GLONASS Satellite-to-Satellite Tracking Instruments (SSTIs), each consisting of an independent receiver and antenna. The measurements of the main onboard GPS receiver (SSTI-A) allowed for Precise Orbit Determination (POD) of the satellite and for gravity field recovery of the low degree and order terms.

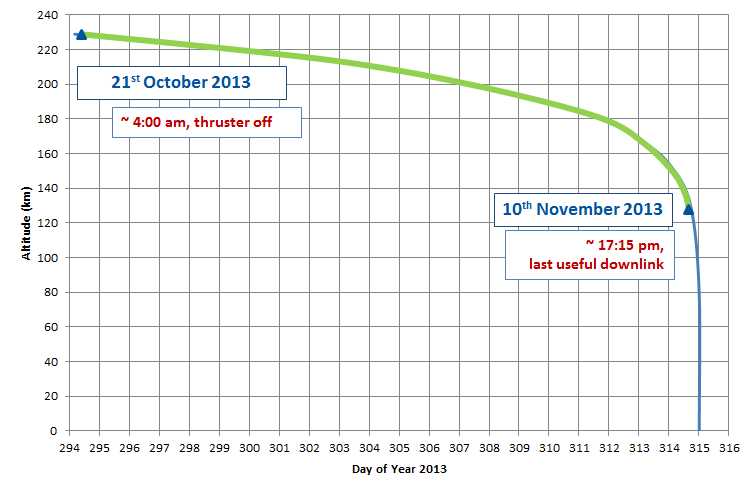
As part of the activities carried out by the Navigation Support Office at ESOC, precise ephemerides of the GOCE satellite have been reconstructed for the entire reentry phase based on the available GPS observations of the onboard LAGRANGE receiver. During the last days of the mission, after GOCE ran out of fuel, it slowly decayed before finally reentering the atmosphere on 11 November 2013. The GPS observations availability during the entire reentry phase provided a unique opportunity for POD to investigate the accuracy of a fully-dynamic approach. The objective was to test the software POD capabilities when accurate non-gravitational forces modeling are included. This was necessary because of the highly aerodynamically perturbed environment expected during the satellite reentry.  All the GPS data available from the moment the thruster was switched off on the 21 October 2013 to the last available telemetry downlink on the 10 November 2013 have been processed, for a total of 21 daily arcs. The analysed period is shown in the figure below, where the green arc defines the period during which GPS observations were available. The results were published and presented in the work of Gini et al. [1].

GNSS processing steps

For the reentry period a dedicated sequence has been defined and implemented within the ESA/ESOC NAvigation Package for Earth Observation Satellites (NAPEOS) software, as shown in the following flowchart. 

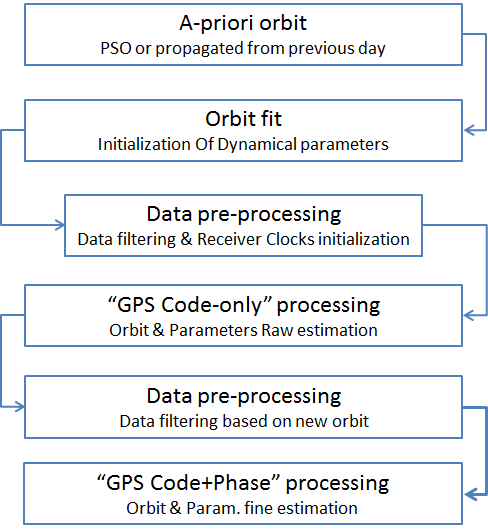
To start the sequence an a-priori orbit was necessary to initialize GOCE’s ephemerides and dynamical parameters. For the first day of the analysed period, 21 October 2013, the Precise Science Orbit (PSO [2]) was used. For the initialization of the following days, the daily arc propagated from the previous day was used instead. An orbit fit of the positions from the a-priori orbit is then performed using 2 different modeling strategies for the non-gravitational forces (aerodynamics and radiation pressure): 1) the standard flat-plate model, where a constant projected area is used to model these forces, and 2) the more accurate ARPA model, based on a ray-tracing technique, described in [3]. As a further step, the GPS data are pre-processed based on the fitted orbit in order to filter the observations and initialize the receiver clocks. After this step an initial orbit determination is performed using only the GPS code information as input. This allows a better initialization of the dynamical parameters and initial state. A meter-level a-priori orbit is also computed as input for the following steps. The GPS data are then pre-processed again based on the new a-priori orbit, filtering the available observations. As a last step the GPS code and carrier-phase data are processed in order to compute the most accurate orbit and parameters.

Results for the reentry phase

The results obtained by this processing chain are shown in the following figures, in terms of post-fit RMS of the GPS carrier-phase residuals on the left and as orbital difference with respect to the PSO solutions on the right.

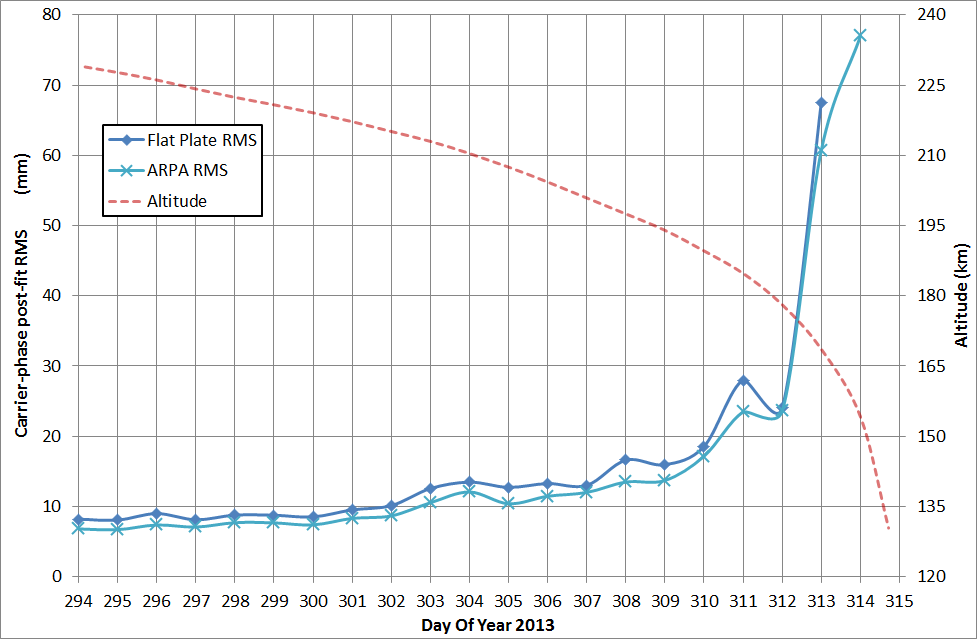
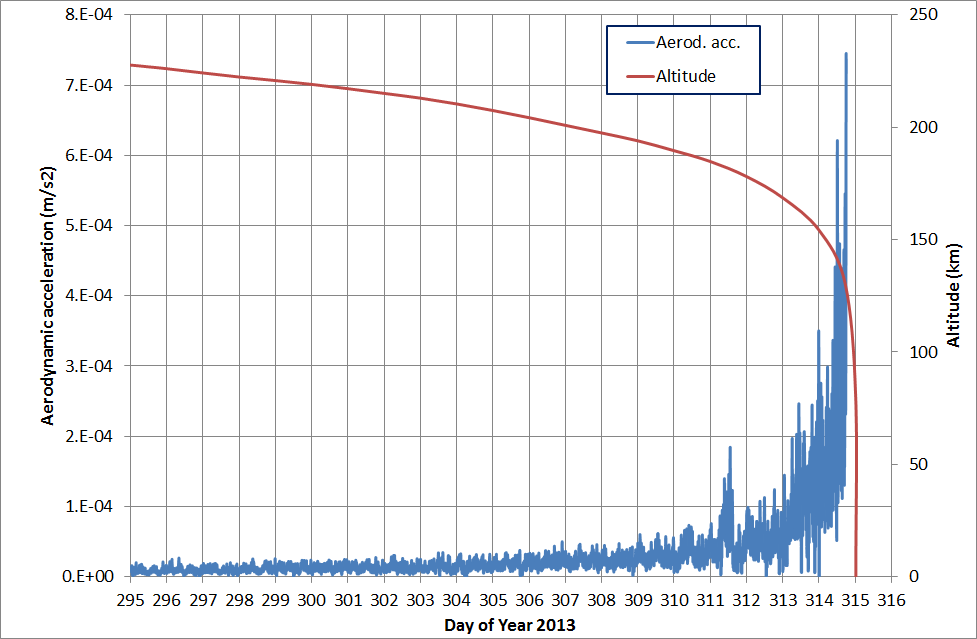
As seen in the figures, the first 16 days show a GPS carrier-phase post-fit RMS between 6 and 14 mm, which then progressively increases up to about 80 mm for the last days with both the flat-plate and ARPA non-gravitational models. This is caused by the aerodynamic accelerations which are progressively increasing with the orbital decay. At an altitude of about 230 km, the aerodynamic forces are not as intense as at the end of the reentry, and the aerodynamic model can adequately absorb these effects. On the other hand, during the last days of the reentry, the aerodynamic effects become significant, causing attitude instabilities. During this last highly-perturbed orbital arcs the aerodynamic models cannot accurately absorb these effects. On the last analysed day, the flat-plate modeling behaved badly, leading to non-convergence of the batch algorithm.

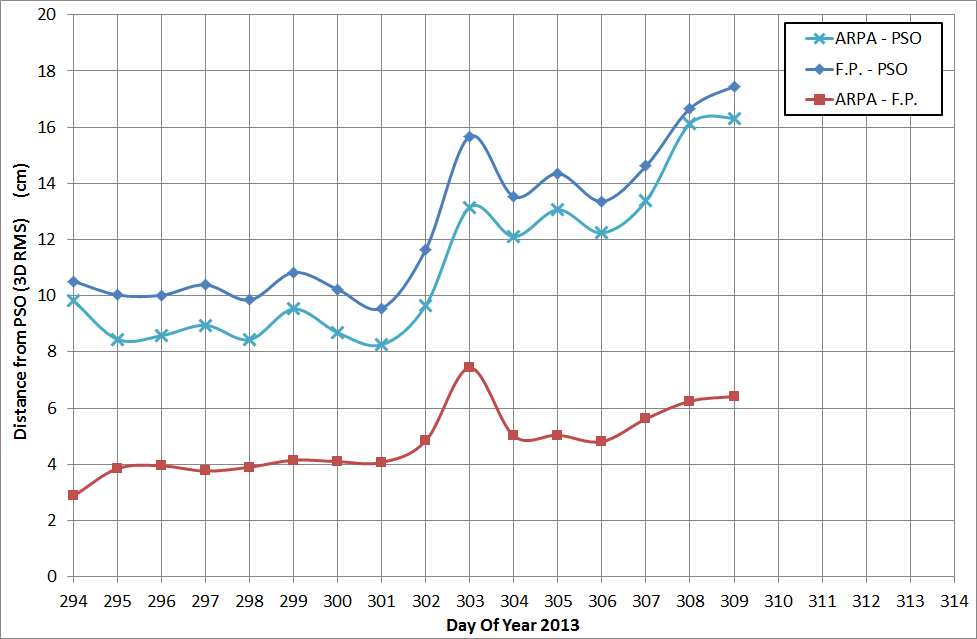
As a validation of the procedure adopted to recover the orbits during the reentry, the computed ephemerides were compared to the PSO solutions. These solutions are based on a reduced-dynamic approach and do not model the non-gravitational perturbations. These perturbations are instead absorbed by empirical accelerations. The result can be seen in the previous figure, on the right-hand side. The PSOs are available until the 5th of November 2013 (Day of Year 309). As can be observed, the difference between the PSOs and the solutions computed with the flat-plate model is around 10 cm for the first 8 days, while with the ARPA model, for the same period, it is around 9 cm. Starting on the 29th of October (Day of Year 302) the difference becomes higher, showing a jump on the DOY 303, reaching the level of about 17 cm for the last day. On the DOY 303 an satellite attitude instability takes place in the yaw angle and this is even more evident in the comparison between the ARPA and flat-plate orbits, which show on DoY 303 a jump to about 7.5 cm, while the average distance is about 4.8 cm.

The following figure gives the idea of how the aerodynamic forces acting on GOCE were growing exponentially during the reentry, highlighting the need for a more accurate modeling of the these forces for the fully-dynamical POD processing adopted for GOCE.

Conclusions

The GPS data of the GOCE on-board LAGRANGE receiver were successfully processed and daily orbital arcs were recovered for all the observed period of the reentry phase, for a total of 21 daily arcs. It has also been possible to further test the ARPA software and its computed non-gravitational forces during the non-drag-free reentry, demonstrating its improvements on the POD solutions.

The post-fit RMS of the undifferenced carrier phase residuals shows values between 6 and 14 mm for the first 16 daily arcs. It then increases with the decrement of the orbit altitude, reaching a level of about 80 mm on the last available day, at an altitude of about 130 km. The estimated empirical accelerations reach higher values at the end of the observed reentry as the altitude of the satellite decreases and the aerodynamic forces increase. With the ARPA modelling, a reduction of these empirical accelerations is observed, with an average decrement of about 20% in the along-track and 40% in the cross-track directions. While the flat-plate aerodynamic model does not take into account all the satellite surfaces, their properties and their interaction with the airflow, the ARPA model significantly reduces this mis-modelling.

The computed final orbits were compared to the Precise Science Orbits, showing a progressively increasing difference as the altitude decreases. The orbits based on the flat-plate model show a difference of about 10 cm for the first 8 days, while the ones based on ARPA shows a value of about 9 cm. For both models a quick jump in the orbital difference is visible for the following days, reaching a value of about 17 cm for the last available PSO. An average difference between the ARPA and flat-plate solutions of about 5 cm has been computed, showing the significant difference between the two modelling approaches. 

References

[1]    Gini F., Otten M., Springer T., Enderle W., Lemmens S., and Flohrer T., PRECISE ORBIT DETERMINATION OF THE GOCE REENTRY PHASE, 5th international GOCE user workshop, Paris 25-28 November 2014

[2]    Bock H., Jäggi A., Meyer U., Visser P.N.A.M., van den Ijssel J., van Helleputte T., Heinze M. and Hugentobler U.; 2011b: GPS-derived orbits for the GOCE satellite. J. Geod., 85, 807-818, doi:10.1007/s00190-011-0484-9.

[3]    Gini F., Bardella M., Casotto S.; 2014: Precise Non-Gravitational Forces modelling for GOCE, Advances in the Astronautical Sciences Spaceflight Mechanics Volume 152